SVM 회귀 - 선형
- SVM 분류와의 차이
- SVM 분류 : 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 한 최대가 되도록 설정
- SVM 회귀 : 제한된 마진 오류(즉, 도로 밖의 샘플) 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 설정
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
#임의의 선형 데이터 생성
np.random.seed(42)
m = 50
X = 2*np.random.rand(m,1)
y = (4+3*X +np.random.randn(m,1)).ravel()
#엡실론에 따른 결정 경계 차이를 확인하기 위해 ε = 1.5 , 0.5 두 모델 생성
svm_reg = LinearSVR(epsilon=1.5, random_state = 42)
svm_reg.fit(X,y)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg2.fit(X,y)
#엡실론보다 큰(결정 경계 밖의 벡터를 찾는 함수)
def find_support_vector(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
#abs : 절대값
return np.argwhere(off_margin)
#argwhere : 해당 데이터의 위치
svm_reg.support_ = find_support_vector(svm_reg, X, y)
svm_reg2.support_ = find_support_vector(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg.predict([[eps_x1]])
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100,1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X,y,"bo")
plt.xlabel("x_1", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
fig, axes = plt.subplots(ncols=2, figsize=(9,4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_reg, X,y, [0,2,3,11])
plt.title(r"$\epsilon = {}$".format(svm_reg.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg.epsilon], "k-", linewidth=2)
plt.annotate(
'', xy=(eps_x1, eps_y_pred), xycoords='data',
xytext=(eps_x1, eps_y_pred - svm_reg.epsilon),
textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
)
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.sca(axes[1])
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
plt.show()
SVM회귀 - 비선형
from sklearn.svm import SVR
np.random.seed(42)
m=100
X = 2 * np.random.rand(m,1) - 1
y = (0.2 + 0.1 * X + 0.5 * X ** 2 + np.random.randn(m,1)/10).ravel()
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg1.fit(X,y)
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="scale")
svm_poly_reg2.fit(X,y)
SVM이론
선형 SVM 분류기 모델은 결정 함수 y 햇을 계산해서 새로운 샘플 x의 클래스를 예측한다. 결괏값이 0보다 크면 예측된 클래스는 양성 클래스 (1)가 되고, 그렇지 않으면 음성 클래스 (0)이 된다.
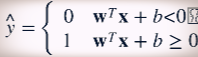
이전 포스팅에서 하드 마진 분류와 소프트 마진 분류에 대해 공부할때 하이퍼 파라미터 C를 변화시켜보며 결정 경계를 확인해보았다.

해당 그래프를 3D 상에 표현해보면

(n개의 특성이 존재할 때 결정 함수h는 n차원의 초평면이고 결정 경계는 n-1 차원의 초평면이다.)
가운데 실선은 결정 함수의 값이 0인 점들로 이루어져 있고, 점선은 결정 함수의 값이 1 또는 -1인 점들로 이루어져 있다. 위의 식을 통해 h(y햇)의 값이 0 이상이면 양성 클래스, 0 미만이면 음성 클래스라고 분류하는 것을 알았다. 즉, 2차원 파란색 단면 (h = 0) 위의 점들은 양성 클래스라고 예측하고 아래의 점들은 음성 클래스라고 예측한다.
(+선형 SVM 분류기를 훈련한다는 것은 마진 오류를 하나도 발생하지 않거나 (하드 마진) 제한적인 마진 오류를 가지면서 (소프트 마진) 가능한 한 마진을 크게하는 w와 b를 찾는 과정이다.)
SVM이론 - 목적 함수
위의 결정 함수 h의 기울기는 가중치 벡터의 노름 ||w||과 같다. (유클라디안 노름, 제곱항을 합한 것의 제곱근 = RMSE)
그러므로 이 기울기를 2로 나누면 결정 함수의 값이 ±1이 되는 결정 경계로부터 2배만큼 멀어진다. 즉, 기울기를 2로 나누는 것은 마진에 2를 곱하는 것과 같다.

쉽게 이야기하면 기울기를 2로 나누면 파란색 선과 w1x1 = 0 사이의 거리 (=가중치 벡터의 노름)가 짧아지므로 마진이 ±1인 지점이 2배만큼 멀어지는 것이다.
마진을 크게 하기 위해서는 ||w||를 최소화해야한다. 마진 오류를 하나도 만들지 않으려면(하드 마진), 결정 함수가 모든 양성 훈련 샘플에서는 1보다 커야하고 음성 훈련 샘플에서는 -1보다 작아야 한다. 이렇게 모든 샘플에 대해 정확히 정의하게 된다면 (정확하게 음성 샘플에서는 h = 0, 양성 샘플에서는 h = 1로 분류) 하드 마진 선형 SVM 분류기의 목적 함수를 제약이 있는 최적화 문제로 표현할 수 있다.

반면에 소프트 마진 선형 SVM 분류기의 목적 함수를 구성하기 위해 각 샘플에 슬랙 변수라는 것을 도입해야 한다. 이때 슬랙 변수 (ζ ≥ 0) 는 해당 샘플이 얼마나 마진을 위반할지 결정하는 변수이다.
소프트 마진 분류기의 목적 함수는 이러한 슬랙 변수를 최소화하여 마진을 위반할 확률을 최소화하는 동시에, 하드 마진과 같이 1/2||w||^2 역시 최소화하는 것을 목표로 한다. 여기에서 하이퍼 파라미터 C가 등장하며 이 파라미터는 두 목표 사이의 트레이드 오프를 결정한다.

SVM이론 - 콰드라틱 프로그래밍
하드 마진과 소프트 마진 문제는 모두 선형적인 제약 조건이 있는 볼록 함수의 이차 최적화 문제이다. (= 콰드라틱 프로그래밍, Quadratic programming, QP)
쉽게 이야기해서 다양한 제약조건이 존재할 경우 가장 최적의 cost function 값을 찾는 것이라고 생각하면 된다.
예를 들어보자.

이라는 함수가 존재할 때 우리의 목표는 해당 cost function을 최적화하는 x1과 x2, 그리고 해당하는 cost function 값을 찾는 것이다. 이를 그래프로 확인해보면

이고 최적점인 빨간점에 대한 x1, x2 그리고 cost function의 값을 찾는 것이다.
x1 = 6.25
x2 = 3.00
cost = 25.4
의 값으로 빨간점에 대한 정보를 구할 수 있겠지만 만약 이 비용 함수에 제약조건이 걸린다면 어떻게 될까?
다음과 같은 제약이 걸려있다고 가정해보자.
- x2 - x1 ≥ 2
- 0.3x1 + x2 ≥ 8
- 0 ≤ x1 ≤ 10
- 0 ≤ x2 ≤ 10
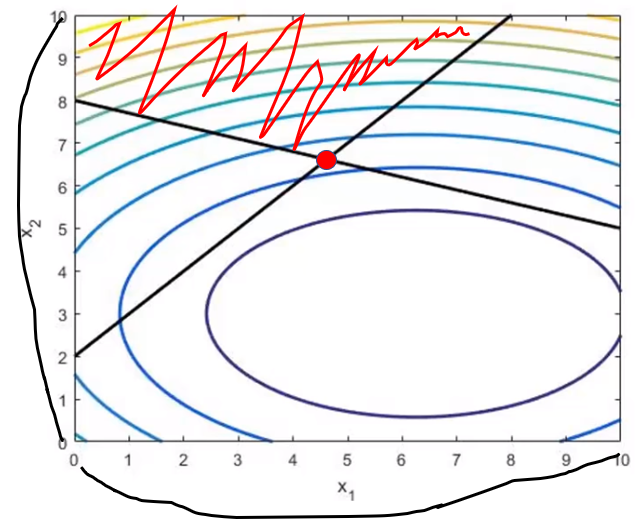
QP는 위의 그림처럼 모든 제약조건을 만족하고 cost function의 최적점인 빨간점을 찾도록 하는 과정이다.
그렇다면 QP 공식과 예시로 보여준 cost function가 어떻게 적용되는지 살펴보자.
우선 QP 공식은 다음과 같다.

그리고 주어진 cost function와 제약조건을 통해 H행렬과 f행렬을 구할 수 있는데,





(+ 제약조건에서 equal 조건이 없으므로 s.t.의 두 번째 조건은 비어있는 벡터로 놓는다.)
이렇게 QP를 구할 수 있다. QP를 사용하면 변수의 수가 많은 경우, 빠르게 해답을 구해야 하는 경우 아주 쉽게 최적의 cost function 값을 구할 수 있게 된다.
'핸즈온머신러닝&딥러닝' 카테고리의 다른 글
| 앙상블 학습 & 랜덤 포레스트 (0) | 2021.06.16 |
|---|---|
| 결정 트리 (0) | 2021.06.14 |
| 서포트 벡터 머신 1 (1) | 2021.06.07 |
| 모델 훈련 4(로지스틱 회귀) (0) | 2021.06.07 |
| 모델 훈련 3(다항 회귀, 학습 곡선, 규제) (0) | 2021.06.02 |